6. どうして分光なのか-2（Lorentzモデル）

多くの物質の誘電関数は, 電子分極励起 ( Lorentz モデル, Tauc-Lorentz モデル, OJL モデル, 調和振動子近似など), イオン分極励起 (調和振動子モデル, Kim 振動子モデルなど), フリーキャリア励起 ( Drude モデル, その拡張モデル) の三つの基本的な励起タイプの組み合わせで記述することができます. ここに列記したいくつかの代表的な誘電関数モデルは, そのほとんどが Lorentz モデルを基に拡張されたものです. ここでは, Lorentz モデルの基本的な性質に触れることにしましょう.

Lorentz モデルは, 正電荷を持つ原子核と負電荷を持つ電子がバネで束縛されているとする古典的なモデルで，量子効果は考慮されません. 光の電場振動 E = E₀ exp ( i ωt) に対して, 質量の大きい原子核は動かず, 電子だけが粘性流体中を振動する物理モデルを仮定しています. 光の電場などの外場から与えられるエネルギーと粘性抵抗で失われるエネルギーが釣り合って安定に振動します.このような振動子を，減衰振動子 ( damped oscillator ) と呼びます. Lorentzモデルの運動方程式は次式で与えられます.

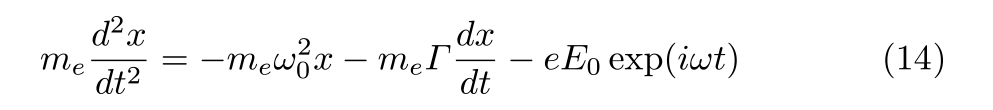
ここで m_e と e は, それぞれ電子の質量と電荷です. 右辺第2項は, 粘性流体中の粘性抵抗を表しており, 運動速度が遅い場合は速度に比例します. Γ は, 粘性抵抗の比例係数で, 減衰係数 ( damping coefficient ) と呼ばれます. 右辺第1項は, 光の電場によって移動した電子がフックの法則 ( F = -k_F x ) に従って復元することを表しています． ここで，ω₀ はバネの共鳴角振動数であり, F = -k_F x から ω₀ = (k_F / m_e)^1/2 と与えられます. 右辺第3項は, exp ( iωt ) で振動する光の交流電場から受けるクーロン力です． (14) 式は, 光の交流電場E₀ exp ( iωt )から電子が受けるクーロン力e E₀ exp ( iωt ) によって電子が加振される減衰振動子の運動方程式です.

図6-1(a) にその運動モデル, (b) に Lorentz モデルから計算される誘電関数を示します.

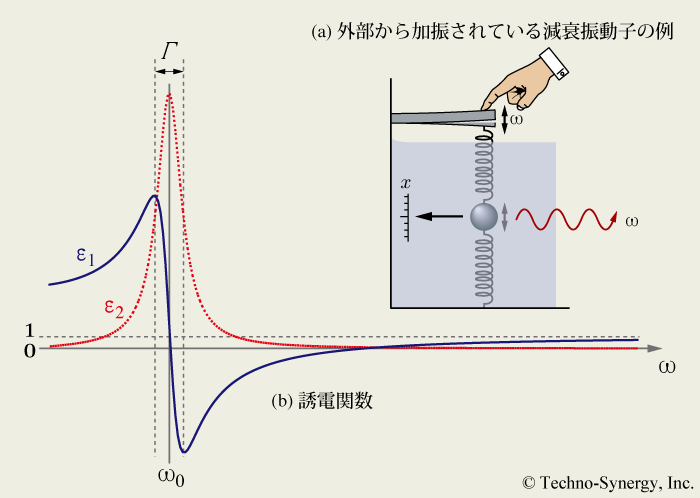
(b)の誘電関数から分かるように, バネの共鳴角振動数 ω₀ で ε₂ が最大になり, ε₂ ピークの半値幅は Γ になっています. ε₂ ピークから遠い領域で ε₁ の勾配が正になる過程を正常分散, ω₀ ±Γ / 2 の領域で ε₁ の勾配が負となる過程を異常分散と呼びます. ここで, (14) 式の解として x ( t ) = a exp ( iωt ) を仮定すると, d ²x / dt² = -aω² exp ( iωt ) およびdx / dt = iaω exp ( iωt ) が得られるので, これらを (14) 式に代入して整理すると次式が得られます.

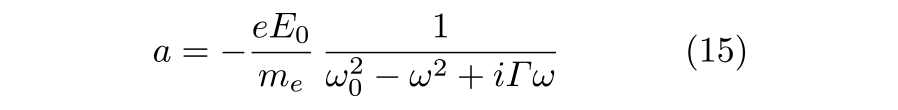
単位体積中の電子の個数を N_e とすると, 分極 P は単位体積中の電気双極子のベクトル和 Σ_i µ_i で表せることから P = -e N_ex (t) となり, x (t) = a exp ( iωt ) の仮定から, P = -e N_e a exp ( iωt ) となります. この P の式を, ε = 1 + P/ ε₀ E に代入すると, 複素誘電率 ε は次式で与えられます.

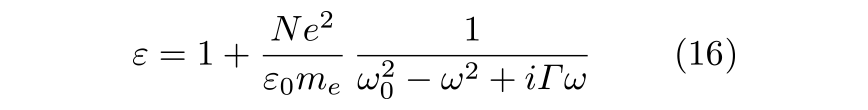
(16) 式がLorentzモデルの基本方程式です.

さらに, 上式の分数の分子と分母に ( ω₀² - ω² - iΓω ) を乗じて整理すると複素誘電率の実部 ε₁ と虚部 ε₂ が得られます.

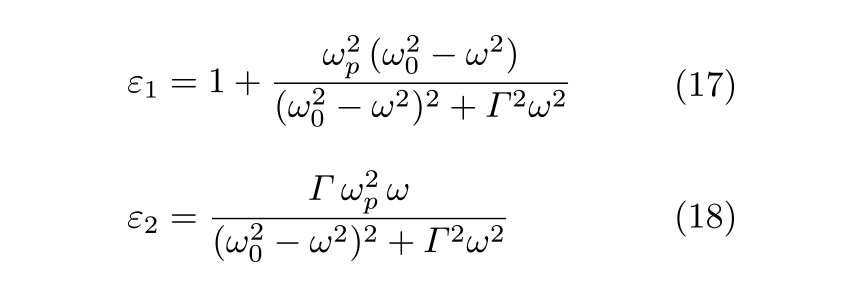
誘電体の紫外から近赤外にかけた波長領域の誘電関数は, 紫外領域における電子分極の共鳴吸収によってほぼ決定されていることは既に述べました. Lorentz モデルおよび Lorentz モデルを拡張した振動子モデルを組み合わせることで, 電子分極の共鳴吸収をモデル化することができ, 紫外から近赤外にかけた波長領域における誘電関数を物理的に正しく表現することが可能になります.
一方, k = 0 と見なせる波長領域における解析では, しばしば(19) 式に示す Sellmeier モデルや, (20) 式に示す Cauchy の分散式 [9] が用いられます．

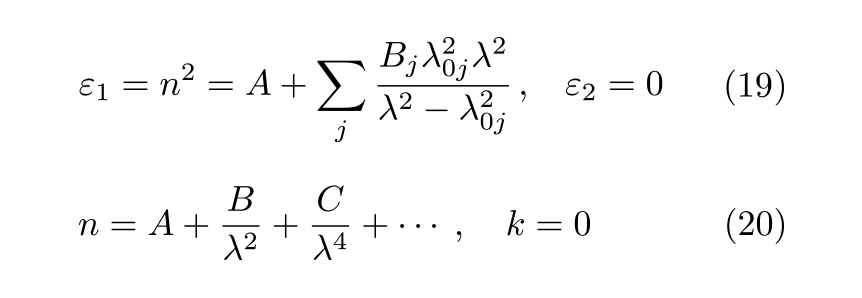
[9] L. Cauchy: "bull. des. sc. maht.", 14, 9 (1830).

ここで, 式中の A, B, C は解析変数です. Sellmeier モデルは, Lorentz モデルの ε₂ ~ 0 に対応し, ω ≪ ω₀ において Γ → 0 を仮定することで導出されます. (19) 式中の λ₀ は, ω₀ に対応する波長です. また, Cauchy の分散式（別名 Cauchy モデル）は, 屈折率 n に関する方程式ですが, Sellmeier モデルの近似式であり, (19) 式を級数展開することで得られます.

Sellmeier モデルや Cauchy モデルは, k = 0 と見なせる解析波長領域で誘電体の膜厚を求める場合や, 解析領域外にある電子分極の共鳴吸収ピークを正確に推測することが難しい場合に有効で, 分光エリプソメーターを誘電体膜の精密膜厚計として使用する場合などに多用されます. しかし, 消衰係数 k も含めて光学定数を求めたい場合には, (19) 式や (20) 式を使用するべきではありません. 図6-1(b) の誘電関数から分かるように, ε₁ と ε₂ (同時に n と κ ) は互いに独立ではなく, ε₁ が変わると ε₂ も変化します. この ε₁ と ε₂ の関係は, クラマース・クローニッヒの関係式 ( Kramers-Kronig relation ) で表されます. クラマース・クローニッヒの関係式は，光が入射することによって物質が応答するという因果律を用いて導出されており, 物理的に正しい誘電関数モデルはクラマース・クローニッヒの関係式を満たします. しかし, Sellmeier モデルや Cauchy モデルでは, ε₂ = 0 を仮定して ε₁ を求めており, クラマース・クローニッヒの関係式を満足していません.

Cauchyの分散式の解析例を示します．

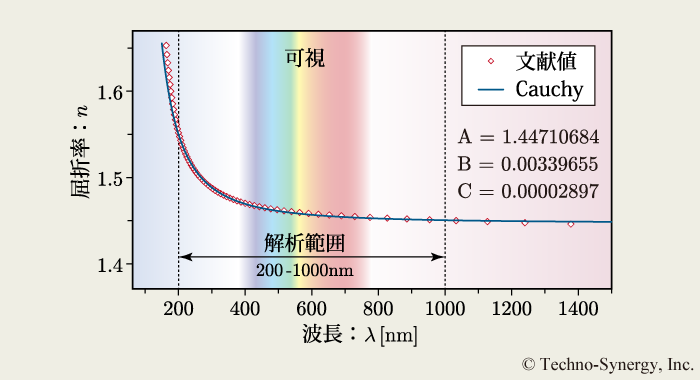
図6-2 は，シリコン酸化膜 （ SiO₂ ） の文献値 [10] ，および解析により求めた SiO₂ の Cauchy の分散式を重ね書きしたものです． Cauchy の分散式は，解析変数を第 3 項目まで用い，波長範囲 200 ～ 1000nm で解析を行いました． 解析変数値は波長に依存するので，解析範囲の取り方を変えると異なった値が得られるので注意が必要です． Cauchy の分散式で表した SiO₂ の屈折率分散モデルは，透明膜と見なせる解析波長範囲で文献値と良く一致しています．

[10] G.E. Jellison, Jr.: "Optical functions of GaAs,GaP, Ge determined by two channel polarization ellipsometry", Opticals Materials, 1 (1998) 151-160.